题目分析
摆动序列是一个典型的贪心问题,这个题目也可以使用动态规划进行求解,下面给小伙伴们展示一下两种算法的实现过程。
DP
我们使用动态规划进行求解,dp[i]表示选择第i个数可得到的最长摆动序列,遍历从0到i - 1的所有数字k,如果nums[i] > nums[k],说明选择第i个数,并且最后状态为上升的最长摆动序列为选择第k个数,并且最后状态为下降的最长摆动序列长度 + 1。小伙伴们可以仔细理解一下,因此我们需要记录两个状态,一个是选择第i个数可得到的最后状态为上升的最长摆动序列长度dp_u,和最后状态为下降的最长摆动序列长度dp_d。可以得到状态转移方程。
$$ dp _ u[i] = \max_{j = 0}^{i - 1} (dp _ u[i], dp _ d[j] + 1) \ \ s.t. nums[i] > nums[j] $$
$$ dp _ d[i] = \max_{j = 0}^{i - 1} (dp _ d[i], dp _ u[j] + 1) \ \ s.t. nums[i] < nums[j] $$
这个方案不难想到,**时间复杂度为$O(n^2)$,空间复杂度为$O(n)$**。
1 | class Solution(object): |
改进DP
当我们换一种思路,使用dp_u[i]记录前i个元素最后状态为上升可得到的最长摆动序列,使用dp_d[i]记录前i个元素最后状态为下降可得到的最长摆动序列。发现并不需要第二层循环,因为当nums[i] > nums[i - 1]时,dp_u[i] = dp_d[i - 1] + 1,而dp_d[i] = dp_d[i - 1]。nums[i] < nums[i - 1]时同理,可得状态转移方程。
$$ dp_u[i], dp_d[i] = \begin{cases} dp_d[i - 1] + 1, dp_d[i - 1] & nums[i] > nums[i - 1] \ dp_u[i - 1], dp_u[i - 1] + 1 & nums[i] < nums[i - 1] \ dp_u[i - 1], dp_d[i - 1] & nums[i] = nums[i - 1] \end{cases}$$
而且我们发现每次只利用到上一次的结果,因此可以使用两个变量保存即可,不用使用两个数组。**时间复杂度为$O(n)$,空间复杂度为$O(1)$**。
1 | class Solution(object): |
贪心
我们思考一种情况,如果存在连续多个下降的数字,那么我们只需要记录最后一个下降的数字即可,它一定是最优的。如1,5 4 3 2 3,在5的时候出现了长度为2的摆动序列,4的时候出现了长度为3的摆动序列,那么后面的3和2都不会影响摆动序列的长度,仅仅当下一次上升时长度才会加1,因此保存最小的数会更容易出现上升。这就是一种贪心思想。**时间复杂度为$O(n)$,空间复杂度为$O(1)$**。
1 | class Solution(object): |
数学解法
数学解法的思维方式也很巧妙,我们要寻找摆动序列的长度,即寻找拐点的数量+2即可。因为去除连续相同数字需要额外保存一个数组,**时间复杂度为$O(n)$,空间复杂度为$O(n)$**。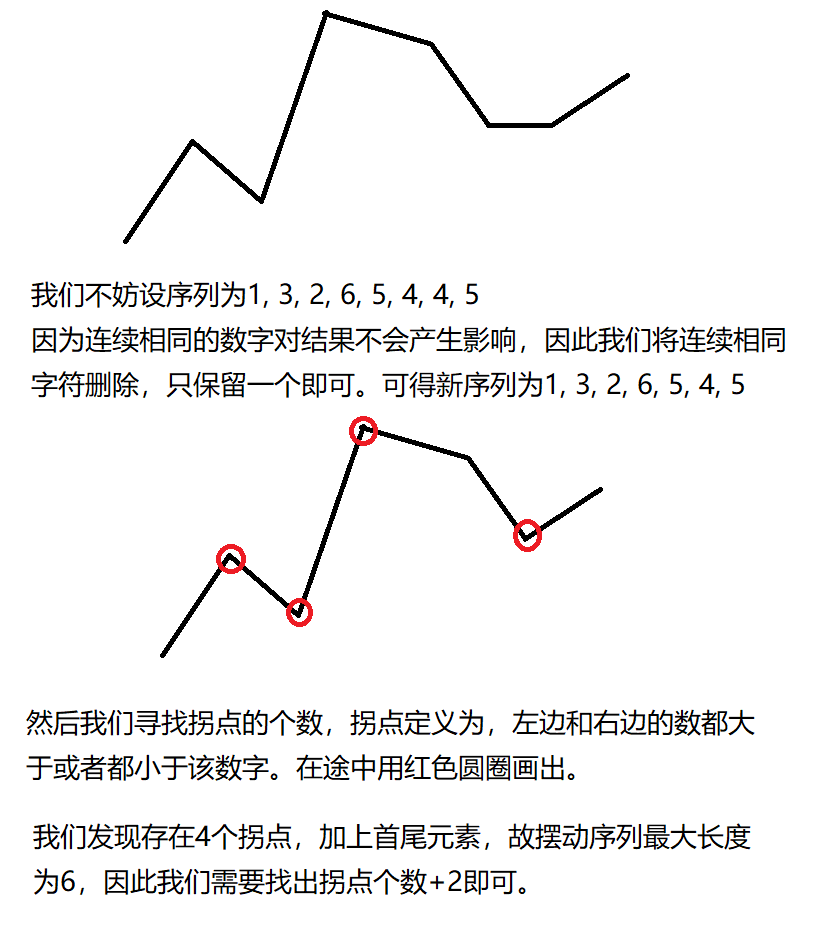
1 | class Solution(object): |
刷题总结
是不是非常有趣,一个题目存在这么多的解法,小伙伴们重点掌握贪心算法和动态规划算法。优化的DP和普通的DP小伙伴们都要掌握,虽然普通DP解这道题目并不是最优方案,但是思路也非常值得我们去学习。